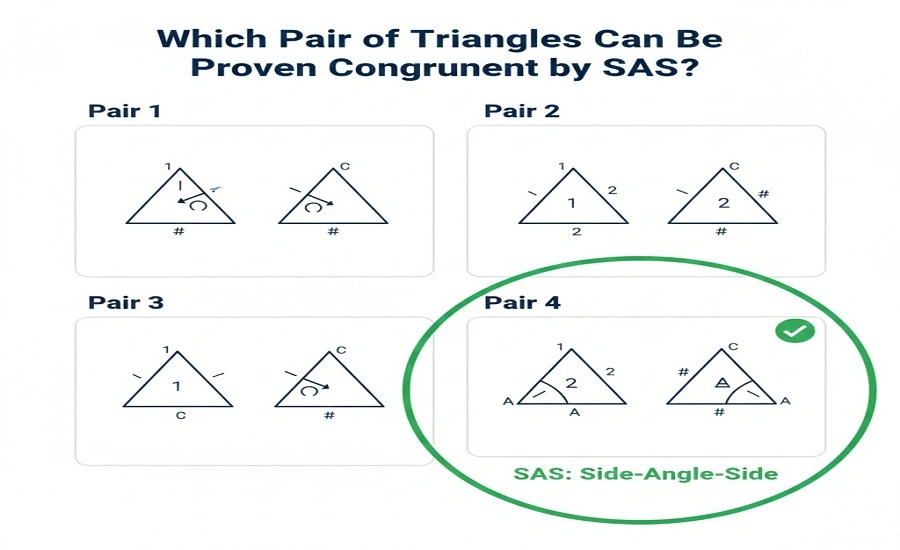
Understanding triangle congruence is a fundamental idea in geometry. One of the maximum crucial congruence guidelines taught in faculties is the SAS Congruence Rule. Many college students regularly ask Which Pair of Triangles Can be Proven Congruent by Sas?
This article presents a clean, step by means of step explanation of the SAS rule, a way to discover it, examples, commonplace mistakes, and solved issues all designed to assist college students, teachers, and exam aspirants grasp the subject.
Table of Contents
What Does Triangle Congruence Mean?
Before answering which pair of triangles can be proven congruent by sas?, it’s far critical to recognize triangle congruence.
Definition of Congruent Triangles
Two triangles are said to be congruent if:
- Their corresponding facets are identical
- Their corresponding angles are equal
- They have the equal form and length
Congruent triangles can be flipped or turned around, but their measurements stay equal.
What Is the SAS Congruence Rule?
The SAS Congruence Rule stands for:
Side – Angle – Side
SAS Rule Definition
If:
- Two aspects of one triangle are identical to
- Two sides of any other triangle, and
- The blanketed perspective among those sides is also identical
👉 Then the two triangles are congruent by using SAS.
This directly answers which pair of triangles can be proven congruent by SAS?
Key Conditions Required for SAS Congruence
Not every pair of triangles qualifies for SAS. The following 3 conditions must be glad simultaneously.
SAS Conditions Table
| Condition | Requirement |
|---|---|
| Side 1 | One side of Triangle A = One side of Triangle B |
| Angle | The included angle must be equal |
| Side 2 | The second side must also be equal |
| Result | Triangles are congruent by SAS |
⚠️ Important:
The angle ought to be among the two given sides.
Which Pair of Triangles Can Be Proven Congruent with the aid of SAS?
The accurate solution to which pair of triangles can be proven congruent by SAS? is:
Any pair of triangles where corresponding sides and the covered angle are equal.
General Example
If:
- AB = DE
- ∠B = ∠E
- BC = EF
Then:
- ΔABC ≅ ΔDEF (by way of SAS)
Visual Representation of SAS Congruence
To apprehend which pair of triangles can be confirmed congruent with the aid of SAS?, don’t forget this shape:
Triangle Pair Example
| Triangle 1 | Triangle 2 |
|---|---|
| AB = DE | Corresponding sides equal |
| BC = EF | Corresponding sides equal |
| ∠B = ∠E | Included angles equal |
| ✅ | Congruent by SAS |
Solved Example: SAS Congruence
Problem:
Two triangles have:
- AB = XY
- AC = XZ
- ∠A = ∠X
Can these triangles be confirmed congruent?
Solution:
- Two facets are equal ✔️
- Included attitude is identical ✔️
✅ Yes, this pair of triangles can be established congruent by using SAS.
Examples of Triangle Pairs Proven by SAS
Example 1: Geometry Diagram Problem
| Given | Observation |
|---|---|
| AB = PQ | Side equality |
| ∠A = ∠P | Included angle |
| AC = PR | Side equality |
| Result | ΔABC ≅ ΔPQR (SAS) |
This is a conventional examination instance of which pair of triangles may be tested congruent with the aid of SAS?
Example 2: Word Problem
Two triangles have:
- Equal bases
- Equal facets
- Angle among them equal
👉 These triangles are congruent by SAS.
Common Mistakes Students Make with SAS
Understanding which pair of triangles can be established congruent by using SAS? also knowing what does NOT qualify.
Common Errors Table
| Mistake | Why It’s Wrong |
|---|---|
| SSA instead of SAS | Angle is not included |
| Different angles | Must be equal |
| Only one side equal | Needs two sides |
| Angle not between sides | Not SAS |
⚠️ SSA is NOT a legitimate congruence rule.
SAS vs Other Congruence Rules
To fully understand which pair of triangles can be proven congruent by sas?, evaluate SAS with different rules.
Triangle Congruence Rules Comparison Table
| Rule | Full Form | Conditions |
|---|---|---|
| SAS | Side-Angle-Side | 2 sides + included angle |
| SSS | Side-Side-Side | All sides equal |
| ASA | Angle-Side-Angle | 2 angles + side |
| AAS | Angle-Angle-Side | 2 angles + non-included side |
| RHS | Right-Hypotenuse-Side | Right triangle only |
Why Is the SAS Rule So Important?
The SAS rule is:
- Easy to use
- Highly dependable
- Frequently used in tests
- Useful in real-existence geometry troubles
This is why questions like which pair of triangles can be demonstrated congruent with the aid of SAS? seem often in faculty assessments, Olympiads, and competitive tests.
Real Life Applications of SAS Congruence
SAS congruence is not simply theoretical.
Real Life Uses
- Architecture – Symmetrical designs
- Engineering – Structural stability
- Surveying – Land measurements
- Robotics – Mechanical precision
Step-by using-Step Method to Identify SAS Congruence
When asked which pair of triangles can be validated congruent via SAS?, follow these steps:
- Identify equal sides
- Check the perspective among them
- Ensure the attitude is included
- Match corresponding parts
- Apply SAS Congruence Rule
Summary Table
| Topic | Key Point |
|---|---|
| SAS Meaning | Side–Angle–Side |
| Required Parts | 2 sides + included angle |
| Validity | Always proves congruence |
| Common Mistake | Using SSA |
| Exam Relevance | Very high |
Main questions to ask on this Which Pair of Triangles Can Be Proven Congruent by using SAS?
1. What does SAS stand for in triangle congruence?
Ans. SAS stands for Side Angle Side, a rule used to prove triangle congruence.
2. Which pair of triangles can be verified congruent with the aid of SAS?
Ans. Any pair of triangles with equal aspects and the protected attitude identical may be confirmed congruent by means of SAS.
3. Why need the perspective to be protected in SAS?
Ans. Because without the blanketed angle, triangles may additionally look one of a kind even though two sides are the same.
4. Is SSA the same as SAS?
Ans. No. SSA is not a legitimate congruence rule, whilst SAS is constantly valid.
5. Where is SAS generally used?
Ans. SAS is widely utilized in college tests, geometry proofs, engineering designs, and production planning.